La bella estate del 2020
Stamattina mi sono preso il tempo di scrivere un post lungo, ragionato e basato sui numeri a proposito delle riaperture estive. Qualsiasi cosa ne pensiate, vi prego di leggerlo fino in fondo prima di commentare.
Mi sono messo a scriverlo perché a proposito dell’estate vedo troppa faciloneria. Leggo: d’estate il virus non circola, l’anno scorso fino a settembre non ce n’era. Oppure: ma se l’anno scorso abbiamo fatto praticamente tutto quello che volevamo, vuoi che quest’anno coi vaccini non facciamo almeno lo stesso? Si dice: ma cosa aspetta il governo ad annunciare la riapertura di tutto da giugno? Nessuno concepisce l’idea di potersi trovare in zona rossa o anche solo gialla, coi ristoranti e le spiagge chiuse, fino ad agosto. Eppure, dal punto di vista strettamente sanitario sarebbe uno scenario realistico, e vediamo perché.
Cominciamo con lo sfatare alcuni miti sull’estate scorsa, grazie al grafico qui sotto. L’anno scorso, quando a inizio giugno si è riaperta la mobilità tra regioni, avevamo circa 300 nuovi casi al giorno, circa 2000 a settimana. In termini del parametro usato oggi per i colori, avevamo 3 (tre) casi settimanali per 100.000 abitanti.
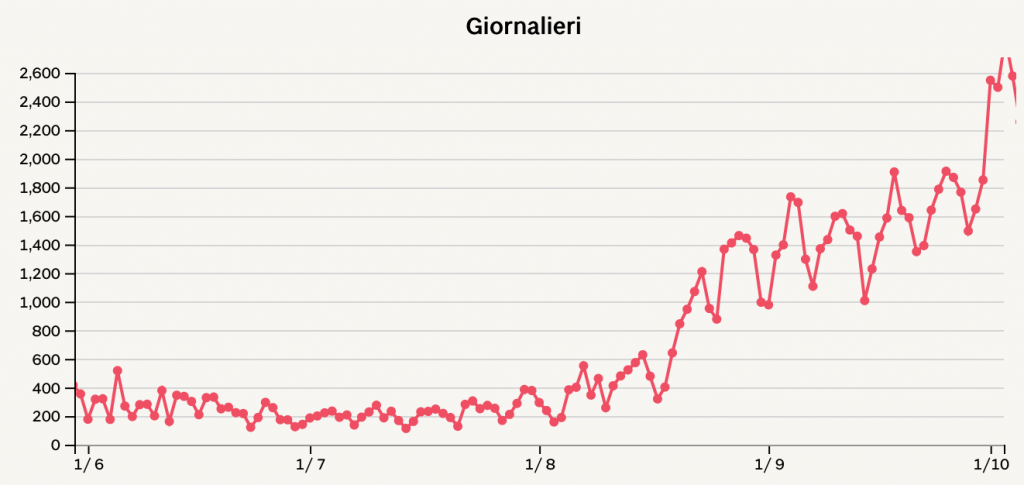
Per confronto, la soglia dell’attuale zona bianca, che dovrebbe dare il via libera a tutto, è 50 casi per 100.000. Anche supponendo che l’estate scorsa ci sfuggissero molti più casi di oggi, parliamo di almeno un ordine di grandezza di differenza. Peraltro, l’unico esperimento di zona bianca coi parametri attuali è stato un disastro: la Sardegna ha retto due settimane. Insomma, l’agognata zona bianca di oggi non ha “pochi casi”; sono comunque tanti.
In termini di andamento, l’anno scorso a giugno l’epidemia ha continuato a ritirarsi, ma non a grande velocità . All’ultima settimana di giugno, quando la gente ha finito di avere paura e ha ricominciato a girare davvero, la discesa si è fermata e il trend si è stabilizzato per un paio di settimane. Abbiamo segnato il minimo di sempre il 14 luglio, con 114 casi. Di lì in poi, però, è subito partita la risalita esponenziale; a fine luglio avevamo 380 casi, a Ferragosto 629, il 23 agosto 1210. Lì abbiamo almeno chiuso le discoteche, e la risalita è rallentata un po’, ma non si è più fermata: 1733 casi il 4 settembre, 1907 il 18 settembre. Poi hanno riaperto le scuole e altra botta verticale: 2844 il 3 ottobre, 5724 il 10 ottobre. Il resto è storia.
Morale: non è affatto vero che d’estate il virus non circola, che il caldo lo uccide, che stando tutti all’aperto non c’è pericolo. Probabilmente l’estate rallenta un po’ il contagio, ma una volta che riapri quasi tutto (comunque l’estate scorsa erano chiusi gli stadi, i concerti, le sagre) l’esponenziale riparte anche in piena estate. Qui stiamo già parlando di riaprire gli stadi l’11 giugno: fate un po’ voi.
E’ indubbio che quest’anno ci sia una grande novità : i vaccini. Ma qual è l’effetto dei vaccini sul contagio? Indubbiamente è forte, come mostrano Israele e Regno Unito – ma solo se sono vaccinati quasi tutti. Peraltro, gli USA e il Cile dimostrano invece che anche a campagna vaccinale ben più avanzata della nostra è possibile una nuova ondata, se si eliminano troppe restrizioni. Nessuno sa ancora bene come funzioni questo effetto in termini quantitativi, ma proviamo a fare un modello.
Supponiamo che il vaccino sia efficace all’80% a prevenire il contagio in ogni forma, anche asintomatica, considerando anche che molti quest’estate avranno avuto una sola dose e quindi che l’efficacia sarà ridotta. Attualmente abbiamo dato almeno una dose a nove milioni di persone; realisticamente, a inizio giugno questo numero potrebbe essere arrivato attorno a venti milioni, forse venticinque se siamo molto bravi. In pratica, circa il 40% degli italiani avrà una probabilità di contagiarsi ridotta dell’80%, il che – supponendo, cosa peraltro non vera, che questi italiani siano mediamente quelli che poi vanno in giro durante l’estate – vuol dire una riduzione della probabilità media di contagio di circa un terzo (0,8*0,4).
Questa è una buona notizia se, come succede in questo periodo di restrizioni colorate, l’Rt è poco superiore a 1; in questo caso, una riduzione di un terzo lo fa scendere sotto 1 e fa spegnere l’epidemia. Se però siamo in condizioni di liberi tutti e tutto aperto, con un Rt di 1,5, 2, 2,5, l’effetto è al massimo quello di rallentare leggermente la crescita esponenziale. In altre parole, anche con la campagna vaccinale attuale, riaprendo tutto a inizio giugno è molto probabile che l’epidemia ripartirebbe rapidamente, come successe l’anno scorso da metà luglio in poi.
A inizio luglio, forse, potremmo essere arrivati a 30-35 milioni di vaccinati con almeno una dose, con una riduzione dell’Rt del 40%; a inizio agosto la riduzione potrebbe essere del 50%. Ma per un virus il cui R allo stato libero è stimato attorno a 3, continuerà a essere ancora troppo poco per eliminare tutte le restrizioni – anche se, da agosto, potrebbe bastare l’effetto delle mascherine, possibilmente FFP2, se solo tutti le portassero davvero.
C’è però ancora un’altra obiezione: visto che l’anno scorso anche con epidemia in espansione abbiamo vissuto tranquilli fino a fine settembre, non potremmo fare lo stesso? Restiamo chiusi fino a inizio giugno, abbattiamo i casi, e poi gestiamo l’estate cercando di non farli risalire troppo e di arrivare a settembre-ottobre, contando che per allora si arrivi alla famosa immunità di gregge; nel momento in cui il fattore di riduzione dovuto ai vaccini superasse i due terzi, si dovrebbe avere Rt minore di 1 anche senza restrizioni e l’epidemia morirebbe.
Bene, allora quanti casi pensiamo di avere a inizio giugno? La settimana scorsa è stata la prima in cui si è visto un calo netto: 20% di nuovi casi in meno rispetto alla settimana precedente, per un totale di “soli” centomila nuovi infetti. Supponiamo di andare avanti così per le sette settimane che ci separano da giugno; vuol dire una moltiplicazione per 0,8^7 = 0,21. In pratica, arriveremmo ad avere circa 21.000 casi settimanali, ossia circa 35 casi per 100.000 abitanti, sufficienti per la zona bianca ma dieci volte superiori a quelli con cui abbiamo riaperto tutto un anno fa.
Attenzione, però; perché noi, invece di tenere duro, dopo una settimana abbiamo già riaperto le scuole, con contestuale candida ammissione del ministro Speranza di come questo avrà un effetto sui contagi. Entro un paio di settimane cominceremo a riaprire a furor di popolo i ristoranti e i teatri. Con questa prospettiva, è difficile pensare che il calo continui a questo ritmo. Se supponiamo che il calo medio nelle prossime settimane sia del 10%, che comunque non è poco, arriveremo a inizio giugno con oltre 50.000 casi a settimana, con l’Italia ancora prevalentemente gialla ma la gente già con il canotto sul portapacchi della macchina.
Ma persino nel caso migliore, riaprire tutto a inizio giugno con 20.000 casi settimanali vuol dire comunque trovarsene magari nuovamente 100.000 a fine luglio. E poi che fai? Certo, i morti non dovrebbero essere molti e gli ospedali dovrebbero essere piuttosto liberi, avendo vaccinato gli anziani, ma bisogna essere pronti a cambiare completamente il nostro approccio.
Già , perché alla fine di questa lunga disamina il messaggio dovrebbe essere chiaro. Non sappiamo niente di certo, e magari quanto sopra si rivelerà completamente sbagliato, e succederà qualche miracolo per cui davvero l’estate farà sparire la malattia. Ma mettendo insieme un po’ di banale matematica e l’umore degli italiani, lo scenario più probabile è che a giugno – o al massimo a luglio, se Speranza tiene duro – si apra comunque tutto, e ci si appresti però a una estate ben diversa dalla scorsa, con il covid in circolazione ovunque e centinaia di migliaia di italiani contagiati, molti asintomatici e in giro. In questo scenario, bisogna essere preparati ad abbandonare il sistema dei colori e a non chiudere niente in nessun caso, nemmeno con numeri che anche solo oggi provocherebbero la zona rossa scura con macchie scarlatte e bubboni neri, e nemmeno con, comunque, decine di morti al giorno, forse anche di più.
Probabilmente è questo lo scenario che ha in mente il governo. Cioé no, un pezzo di governo secondo me pensa davvero di tenere chiuso fin che non arriviamo a cento casi al giorno, ma sono dei pazzi e finiranno politicamente linciati entro breve. Ma per il resto, questa mi sembra la strada più probabile; capite però perché il governo esiti ad annunciarla apertamente, visto che comunque c’è anche una grossa parte di Paese che si chiude in casa, invoca il manganello sui ristoratori e chiama i vigili se il vicino riceve due amici.
P.S. Come corollario, se avete più di sessant’anni io vi consiglio comunque di pianificare vacanze solo in luoghi ben isolati. Se non sarete vaccinati rischierete grosso, e se lo sarete, davvero volete rischiare di essere in quello sfortunato 5% su cui il vaccino ha poco effetto? Vedete voi.